
Sir Roger Penrose, an authority on various achievements in space physics, won the 2020 Nobel Prize in Physics for discovering that black hole formation supports the theory of general relativity. He is known to have devised impossible objects such as the Penrose triangle. He says that even before the Big Bang, other universes exist and can still be observed.
The Big Bang thinks like the beginning of the universe, but even before the Big Bang, another universe exists and its traces can still be observed. The Big Bang wasn’t the beginning, but something existed before the Big Bang, and it can be said that our future exists. The present universe repeatedly expands and goes to all mass decay, but his theory argues that the big bang by other forces is in the distant future.
It is a trace of an extinct black hole and a trace of the universe that is thought to exist as the Hawking Point, an area where strong electromagnetic waves are observed. Penrose mentioned 20 Hawking Points in a 2019 study, but the 2020 study argues that there is convincing evidence that at least 6 Hawking Points exist in the cosmic microwave background (CMB). If Penrose presents the theory of Hawking Point in CMB at the Royal Astronomical Society and the existence of Hawking Point is proven, the existence of the pre-Big Bang universe can be more certain.
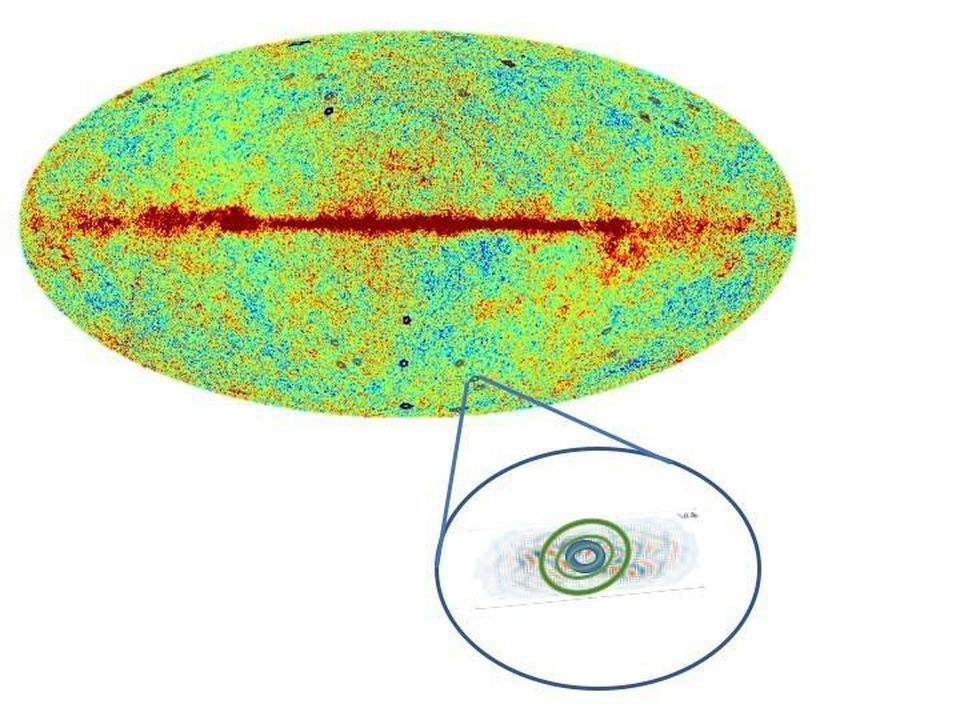
Like Penrose’s argument, opinions are divided that there is room for support and debate over the theory that there is a possibility that a new big bang may occur after the universe contracts during repeated expansion and converges to a dimensionless singularity.
Penrose, along with Stephen Hawking, is also known to prove the singularity theorem in which all the laws of nature known to reach infinite mass by causing an object to undergo gravitational collapse at high density will disappear. Penrose and Hawking’s theorem on singularity is the most important contribution after Einstein to the theory of relativity. Related information can be found here .

